Pemodelan Multi Skenario dan Rekomendasi Strategi Pengendalian Penyebaran Virus Corona di Indonesia

oleh

Budi Sulistyo, Senior Data Scientist PT. SHARING VISION INDONESIA,

Dimitri Mahayana, Dosen STEI Institut Teknologi Bandung, Kelompok Keahlian Kendali dan Komputer,

Dan Tim Data Scientist PT. SHARING VISION INDONESIA

Abstrak:

Artikel mencoba menjelaskan fenomena wabah Corona di Indonesia dengan pemodelan sistem dinamik. Sistem dinamik dengan persamaan diferensi orde 30, nonlinier dengan umpan balik positif telah digunakan untuk memodelkan fenomena wabah Corona di Indonesia. Beberapa skenario kontrol yang dilakukan oleh masyarakat atas instruksi pemerintah disimulasikan. Validasi  dilakukan dengan melihat kesesuaian dengan data yang ada dan model kurva Richard untuk pandemi. Hasil simulasi sementara menunjukkan, physical distancing yang ketat yang memperkecil laju penularan sekecil mungkin disertai dengan deteksi dini yang cepat sangat efektif untuk memperkecil dampak wabah Corona di Indonesia. Dengan konsitensi dan kebersamaan melaksanakan physical distancing dalam rangka memperkecil laju penularan disertai dengan deteksi dini yang cepat, jumlah total masyarakat yang terinfeksi diharapkan ada pada kisaran belasan ribu orang dan wabah bisa segera berakhir . Namun kelemahan masyarakat dan pemerintah dalam melaksankana physical distancing maupun deteksi dini yang lambat akan menjadikan jumlah penderita yang terinfeksi wabah Corona di Indonesia bisa melewati angka psikologis satu juta orang, membuat Indonesia berpotensi menjadi episentrum baru wabah ini, dan wabah ini akan berlangsung jauh lebih lama. Penulis merekomendasikan pemerintah dan masyarakat bahu membahu dalam menekan wabah ini, misalnya dengan kebijakan yang lebih pasti dan lebih tegas berkenaan dengan memastikan laju penularan seminimal mungkin dan membuat deteksi dini secepat mungkin.

1. Pendahuluan

Hari ini, 25 Maret 2020, akumulasi kasus terjangkit yang dilaporkan adalah 790 kasus, 58 meninggal dan 31 sembuh. Kecepatan penularan virus ini sungguh luar biasa. Grafik akumulasi jumlah terjangkit menampakkan pola menanjak secara eksponensial. Data global menunjukkan kenaikan dengan kelipatan 1,23 kali, dalam dua hari dari tanggal 20/3 (274696) ke tanggal 22/3 (336934). Angka-angka ini secara natural memang akan bergerak dengan pola demikian. Artinya, jika kita tidak melakukan kontrol, angka ini akan naik terus secara eksponensial.

Langkah apa saja yang dapat kita lakukan untuk menekan kenaikan ini? Apakah angka total terjangkit dapat kita tekan dengan tindakan kontrol tertentu? Apakah kita dapat mempersingkat rentang waktu siklus penyebaran virus ini? Model dinamika penyebaran virus yang dibahas dalam tulisan ini diharapkan menjadi bagian kecil dari berbagai upaya yang telah dilakukan sebelumnya untuk mencari titik terang guna menjawab pertanyaan-pertanyaan tersebut. Harapannya, dengan model ini kita dapat memiliki gambaran, meskipun kasar, mengenai perilaku sistemik dari penyebaran wabah. Lebih jauh lagi, model ini juga dirancang untuk dapat mensimulasikan berbagai skenario pengendalian yang mungkin dilakukan.

Tulisan ini akan memaparkan beberapa hasil simulasi penanganan wabah korona. Tujuannya adalah agar kita memperoleh gambaran kasar mengenai kondisi saat puncak dan akhir siklus. Simulasi ini juga diharapkan dapat memperkirakan kapan siklus akan berakhir berdasarkan skenario tertentu

2. Simulasi Skenario Physical Distancing

Simulasi menunjukkan bahwa skenario pengendalian dengan physical distancing yang sangat disiplin dapat menurunkan batas atas akumulasi confirmed case  dan memperpendak durasi siklus wabah yang terjadi. Longgar sedikit saja, maka hasilnya bisa jauh berbeda. Di bagian ini kita akan mensimulasikan tiga skenario physical distancing, yakni skenario ketat, moderat dan longgar. Simulasi ini dilakukan dengan beberapa asumsi tambahan mengenai delay dirilisnya confirmed case dan isolasi eksisting yang telah dilakukan. Asumsinya adalah sebagai berikut:

1. Adanya delay dalam dirilisnya confirmed case. Delay diasumsikan sangat moderat hanya selama rata-rata tiga hari. Delay ini adalah jeda waktu sejak saat dilakukannya tes terhadap seseorang (suspect), yang kemudian dinyatakan positif, hingga konfirmasi resmi pemerintah yang  memasukkan orang tersebut ke dalam akumulasi total terjangkit. Semakin panjang delay actual maka semakin besar gap antara confirmed case yang diumumkan dengan kondisi aktual.
2. Deteksi dan isolasi hanya dapat menjaring 40% terjangkit setelah fase inkubasi. Ini karena dalam masa inkubasi peluang deteksi sangat rendah terhadap seseorang yang aktualnya telah terjangkit. Selain itu, berdasarkan pernyataan beberapa sumber,  terdapat 40% – 60% terjangkit aktual yang hanya menampakkan gejala sakit sangat ringan atau bahkan tanpa gejala sama sekali.
3. Dalam simulasi ini Physical distancing yang saat ini telah dilakukan dianggap mulai berjalan efektif pada tanggal 30-maret-2020.

2.1. Simulasi Skenario Physical Distancing Ketat

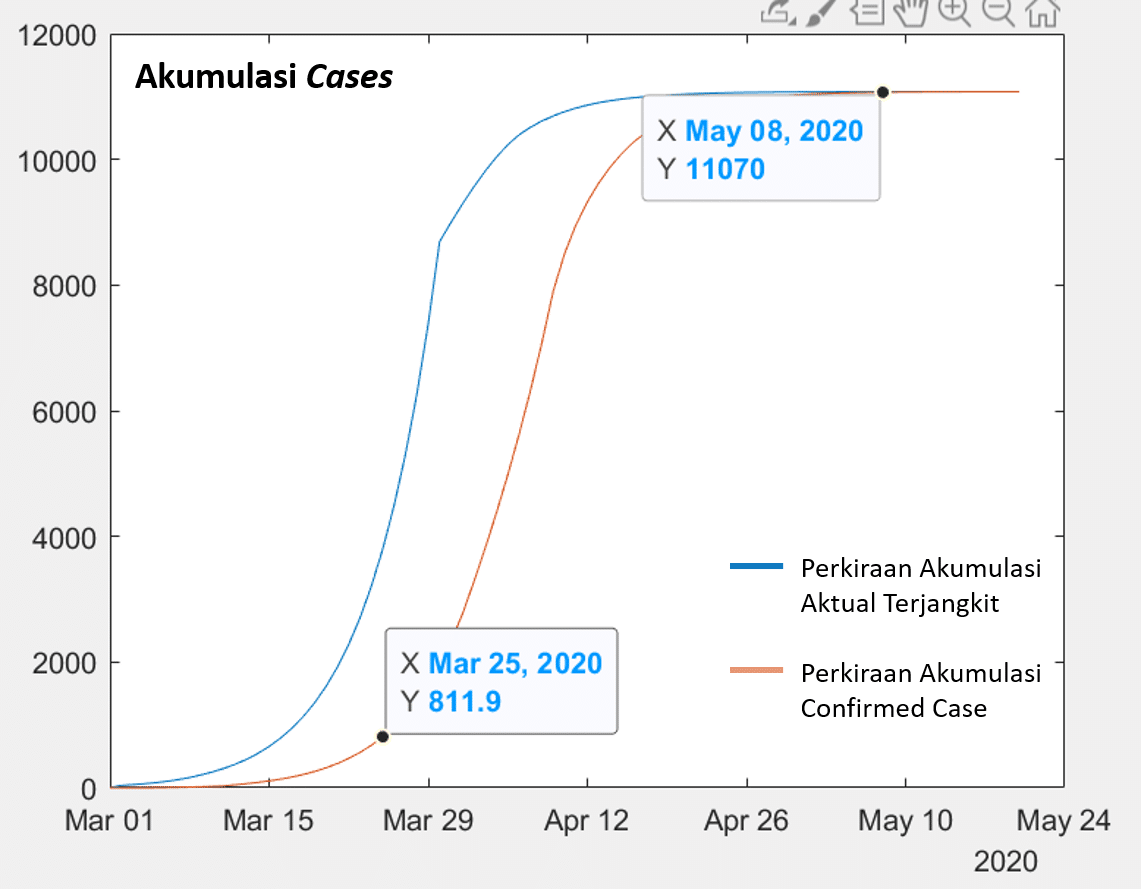
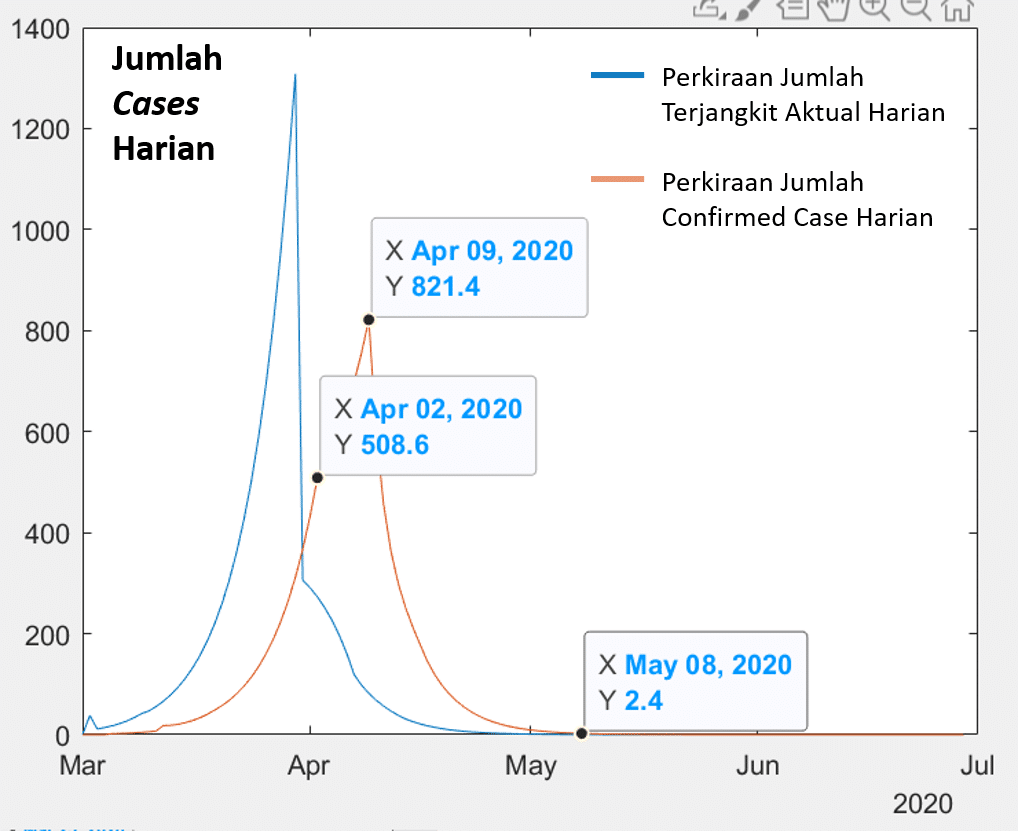
Physical distancing ini dapat menurunkan secara drastis batas atas akumulasi confirmed case dan sekaligus memperpendek durasi siklus. Syaratnya adalah, mekanisme social distancing harus dapat menurunkan laju penularan oleh setiap orang terjangkit hingga tinggal 1/5 dari laju awalnya. Langkah praktisnya adalah, setiap orang harus memastikan bahwa dia sudah menurunkan peluang penularan virus dari dirinya ke orang lain atau dari orang lain ke dirinya hingga tinggal 1/5. Apa artinya? Jika seandainya seseorang berpotensi menularkan virus ini ke 1 orang per hari, maka dia harus memastikan bahwa kontrol yang dilakukan dapat menurunkan menjadi hanya 1 orang dalam 5 hari. Dengan asumsi ini maka kita mendapatkan bahwa akhir siklus akan terjadi pada minggu pertama Mei dengan jumlah akumulasi confirmed case sekitar 11 ribu orang. Puncak kasus akan terjadi pada minggu pertama April dengan 821 confirmed case baru per hari (Gambar 1). Perlu diingat bahwa skenario ini  pada dasarnya sangat optimis yaitu mengasumsikan bahwa kita dapat melakukan physical distancing yang ketat dan upaya proteksi lainnya yang dapat menurunkan kecepatan penularan 1/5 kali dari kondisi sebelumnya.

• 

• 

Gambar 1 Skenario physical distancing ketat dimulai tanggal 30-Maret-2020

2.2. Simulasi Skenario Physical Distancing Moderat

Simulasi berikutnya akan menunjukkan bahwa jika kita tidak mampu melakukan skenario physical distancing ketat dan hanya dapat menerapkan sampai tingkat moderat, maka hasilnya akan sangat jauh berbeda. Dalam skenario ini, anggap saja kita hanya mampu menurunkan kecepatan penularan hanya ½ kali dari nilai awalnya. Perlu sangat kita waspadai bahwa karakteristik dari sistem dengan umpan balik positif yang tidak stabil adalah bahwa perbedaan sedikit saja dalam parameter akan menghasilkan hasil akhir yang jauh berbeda.

• 

• 

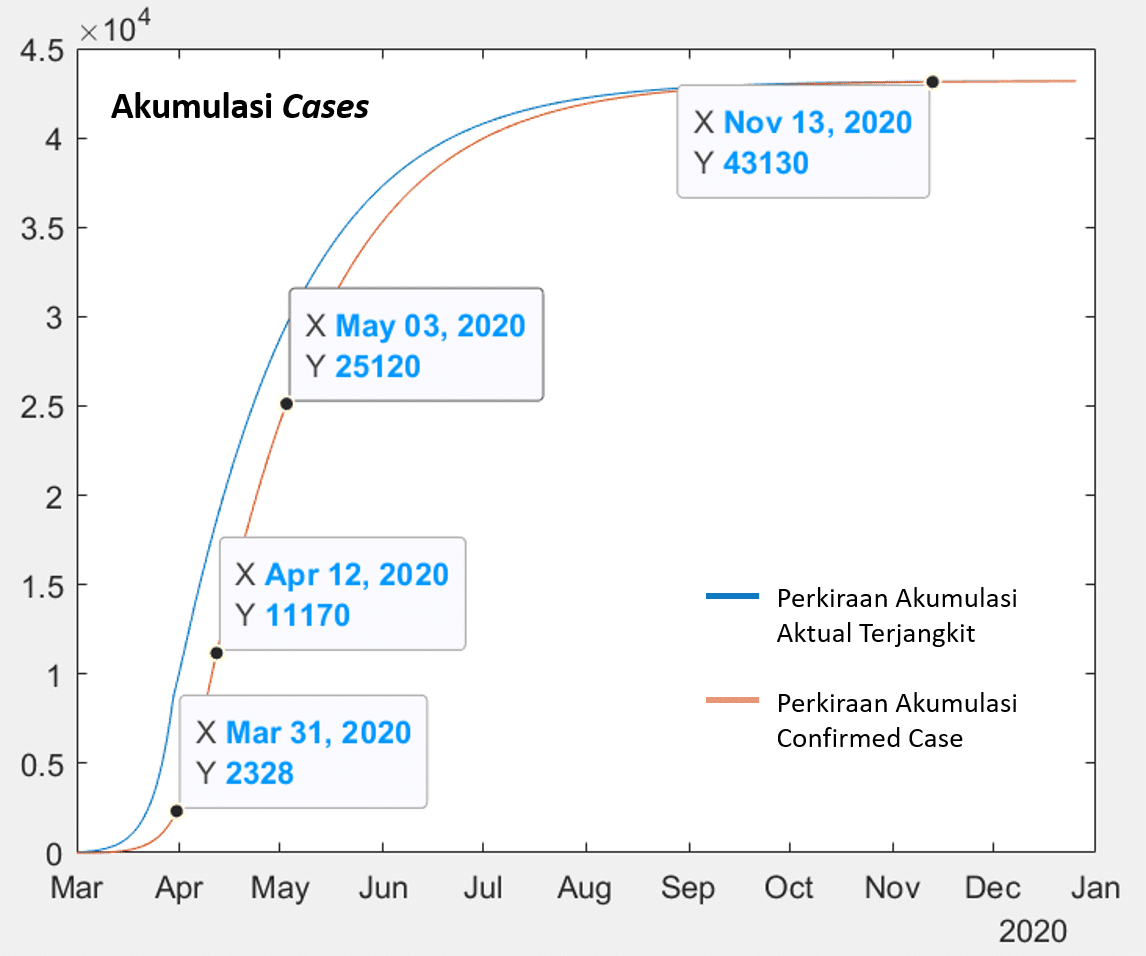
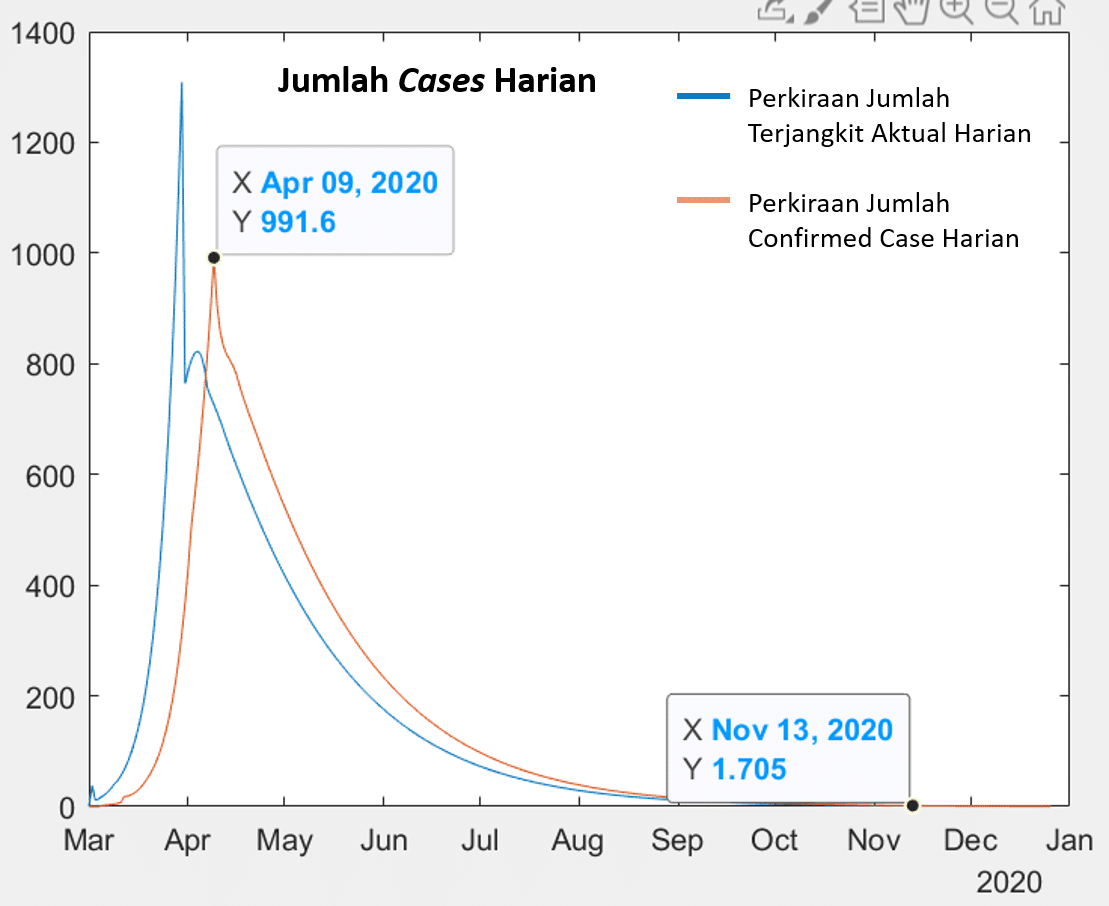
Gambar 2 Skenario physical distancing moderat dimulai tanggal 30-Maret-2020

Tampak bahwa siklus akan menjadi sangat panjang hingga minggu kedua November dengan akumulasi confirmed case hingga 43 ribuan. Puncak siklus akan terjadi pada 9 April dengan 990-an confirmed case per hari dan selanjutnya menurun secara gradual hingga menjadi 2  confirmed case per hari di akhir siklus.

2.3. Simulasi Skenario Physical Distancing Longgar

Di bagian ini kita akan mensimulasikan apa yang akan terjadi jika kita ternyata gagal menerapkan physical distancing moderat dan hanya mampu mengurangi sedikit laju penularan. Kita asumsikan bahwa kita hanya mampu menekan laju penularan menjadi 7/10 atau 70% kali dari nilai awalnya, maka kita dapatkan hasil simulasi berikut ini:

• 

• 

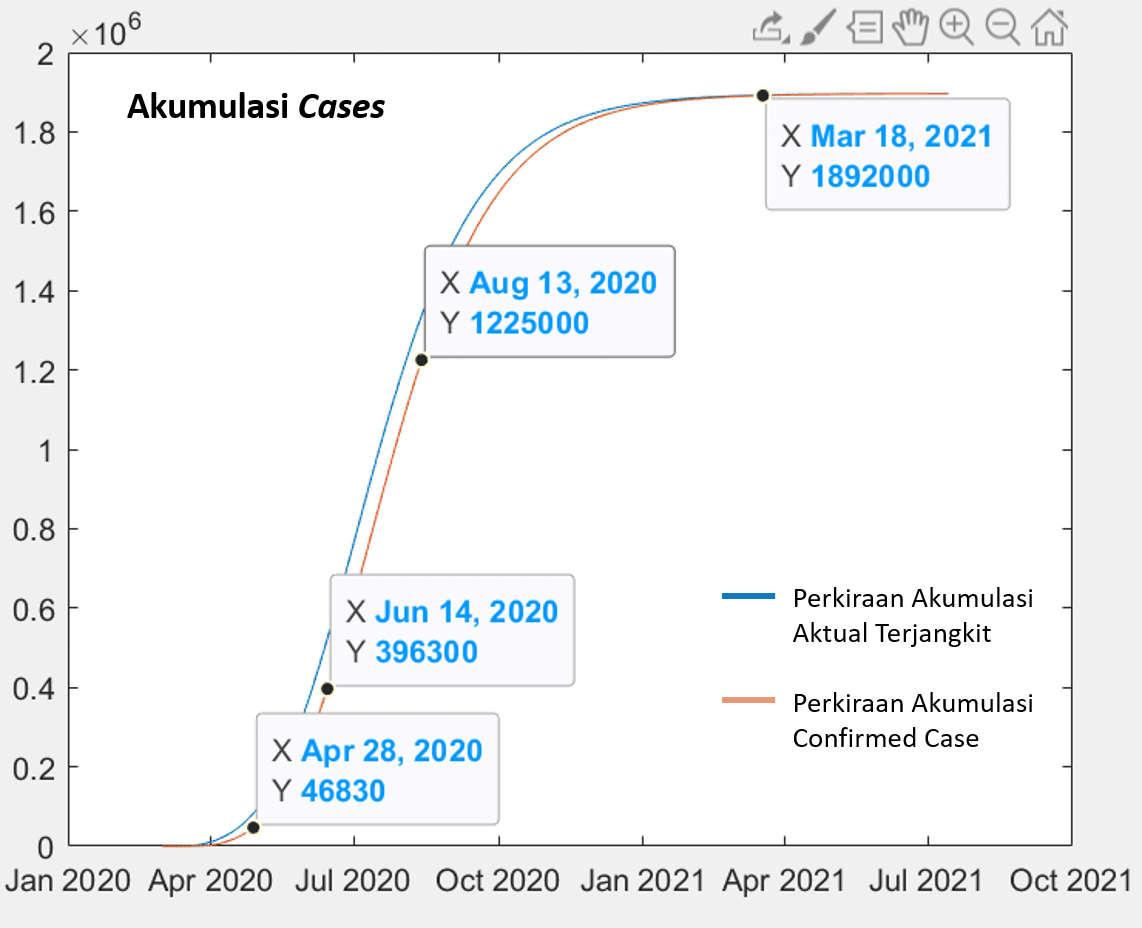
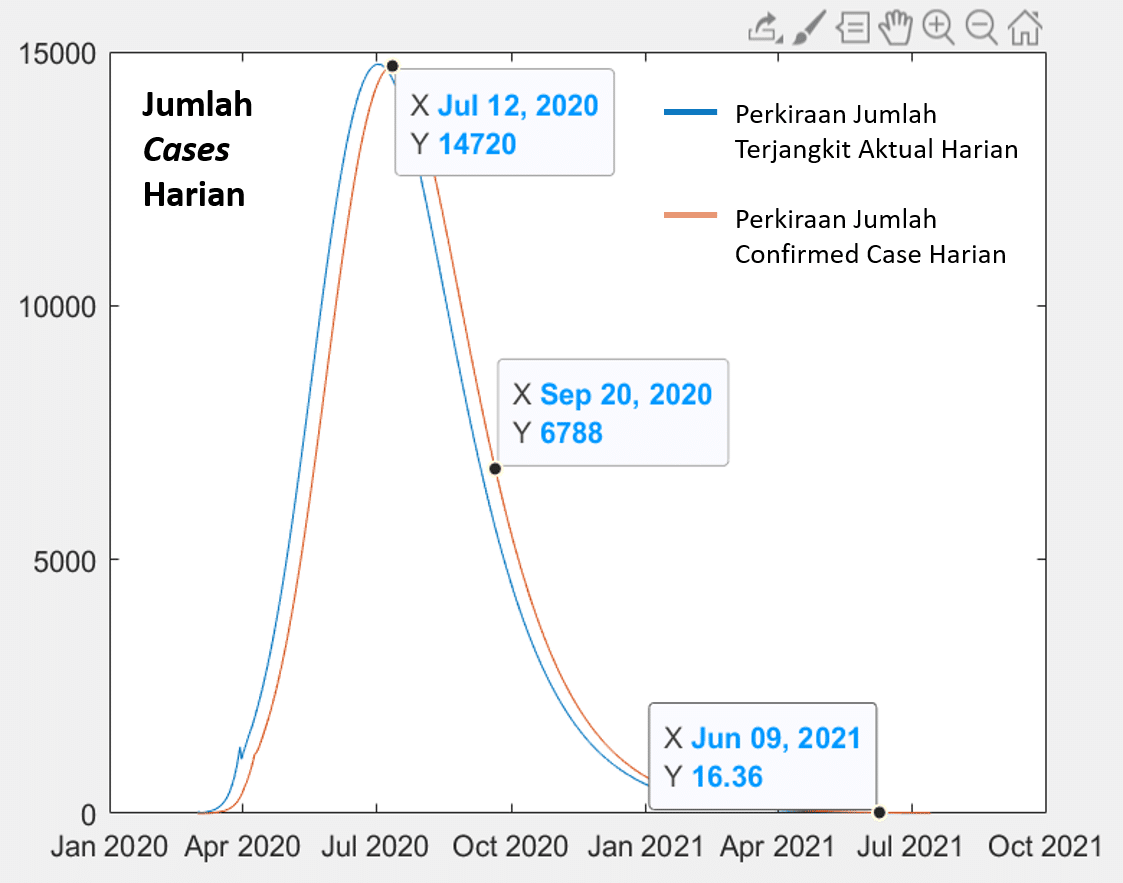
Gambar 3. Skenario physical distancing longgar dimulai tanggal 30 Maret 2020

Tampak bahwa kita akan mengalami siklus yang luar biasa panjang hingga 18 Maret 2021 dengan batas angka confirmed case sudah mendekati 1.9 Juta orang. Puncak siklus terjadi di tanggal 12 Juli 2020 dengan angka harian confirmed case mencapai 14720 kasus per hari. Ini tentu akan menjadi bencana yang sangat luar biasa!

3. Simulasi Skenario Perluasan Cakupan Deteksi dan Isolasi.

Dalam skenario ini kita hanya menjalankan strategi perluasan deteksi dan isolasi, termasuk deteksi terhadap orang terjangkit di fase sangat awal. Saat ini pemerintah sudah cukup proaktif untuk mengkategorikan seseorang yang berisiko tinggi positif ke dalam kategori ODP dan PDP. Deteksi dan isolasi semacam ini juga dapat memperpendek siklus wabah serta menurunkan batas atas akumulasi terjangkit. Anggap bahwa kita bisa mendeteksi dan mengisolasi 20% orang terinfeksi yang masih berada di fase awal (minggu pertama), 50% terjangkit di fase tengah dan akhir (minggu kedua, ketiga dan keempat). Dalam simulasi bagian ini kita meniadakan dulu strategi physical distancing.

• 

• 

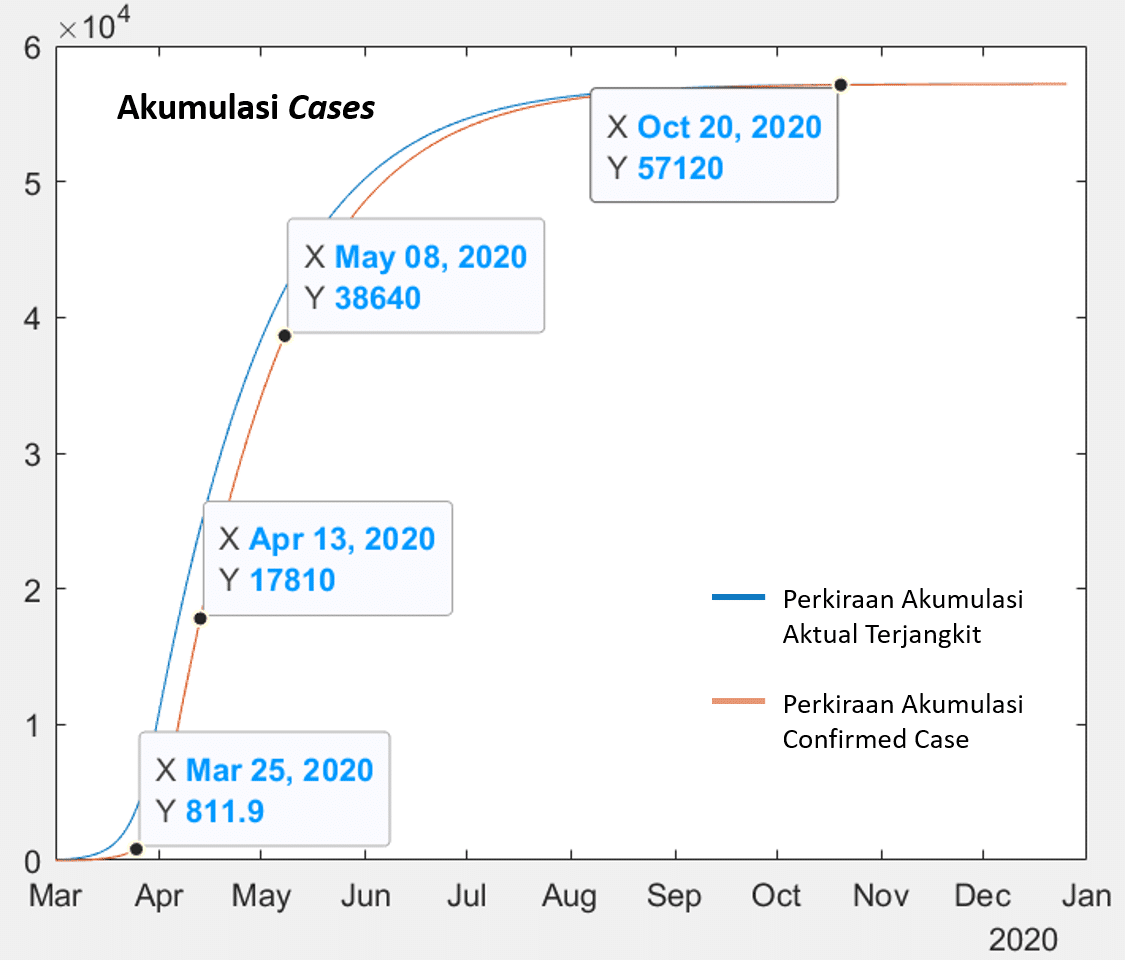
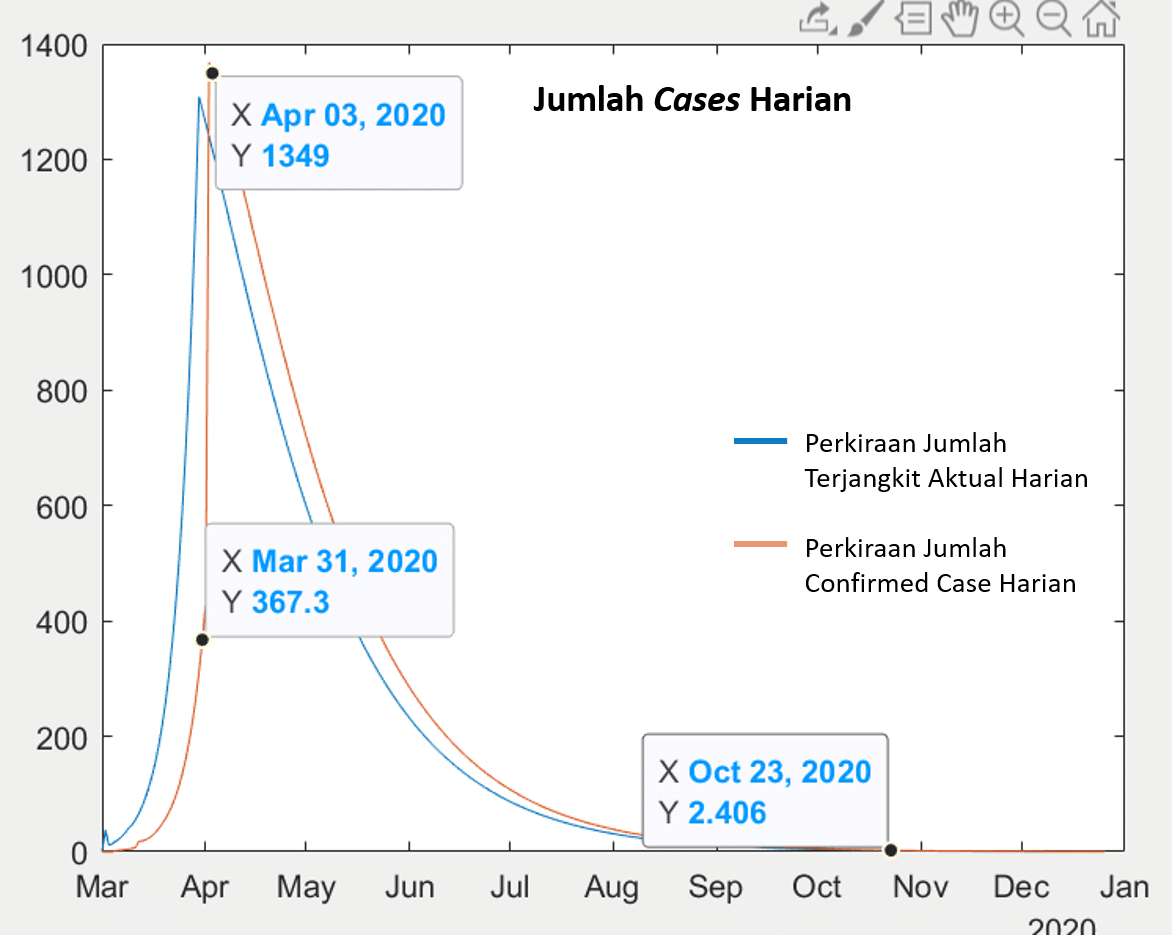
Gambar 4 Skenario perluasan deteksi dan isolasi (termasuk deteksi dini)

Dengan hanya menjalankan skenario ini, siklus wabah akan berakhir di minggu ketiga Oktober dengan batas atas akumulasi confirmed case sekitar 57 ribu orang. Puncak siklus akan terjadi pada minggu pertama April dengan jumlah confirmed case harian di sekitar 1350 orang. (Gambar 4).

4. Simulasi skenario gabungan physical distancing moderat dan perluasan deteksi serta isolasi

Dalam skenario ini kita akan mencoba menggabungkan dua jenis kontrol yang dilakukan dalam dua skenario sebelumnya. Anggap bahwa dua jenis kontrol ini kita mulai dengan konsisten sejak tanggal 30-Maret-2020. Dua jenis kontrol tersebut adalah:

1. Penurunan kecepatan penularan oleh satu orang yang positif dianggap bisa ditekan hingga ½ dari nilai awalnya mulai tanggal 30-Maret.
2. Perluasan deteksi dan isolasi untuk 20% orang terinfeksi yang masih berada di fase awal (minggu pertama), 50% terjangkit di fase tengah dan akhir (minggu kedua, ketiga dan keempat).

Maka kita dapatkan hasil simulasi berikut ini:

• 

• 

Gambar 5 Hasil simulasi skenario physical distancing moderat dengan perluasan deteksi serta isolasi (termasuk deteksi dini)

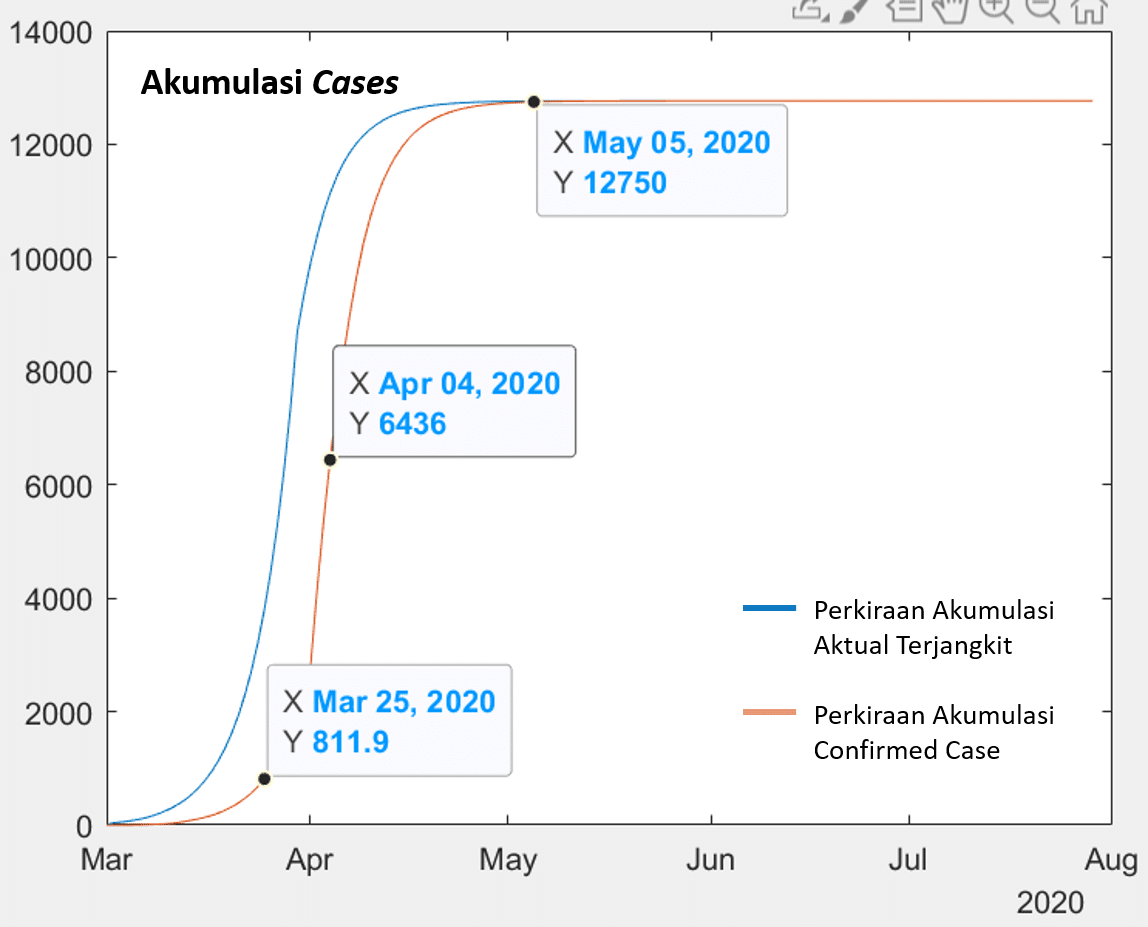
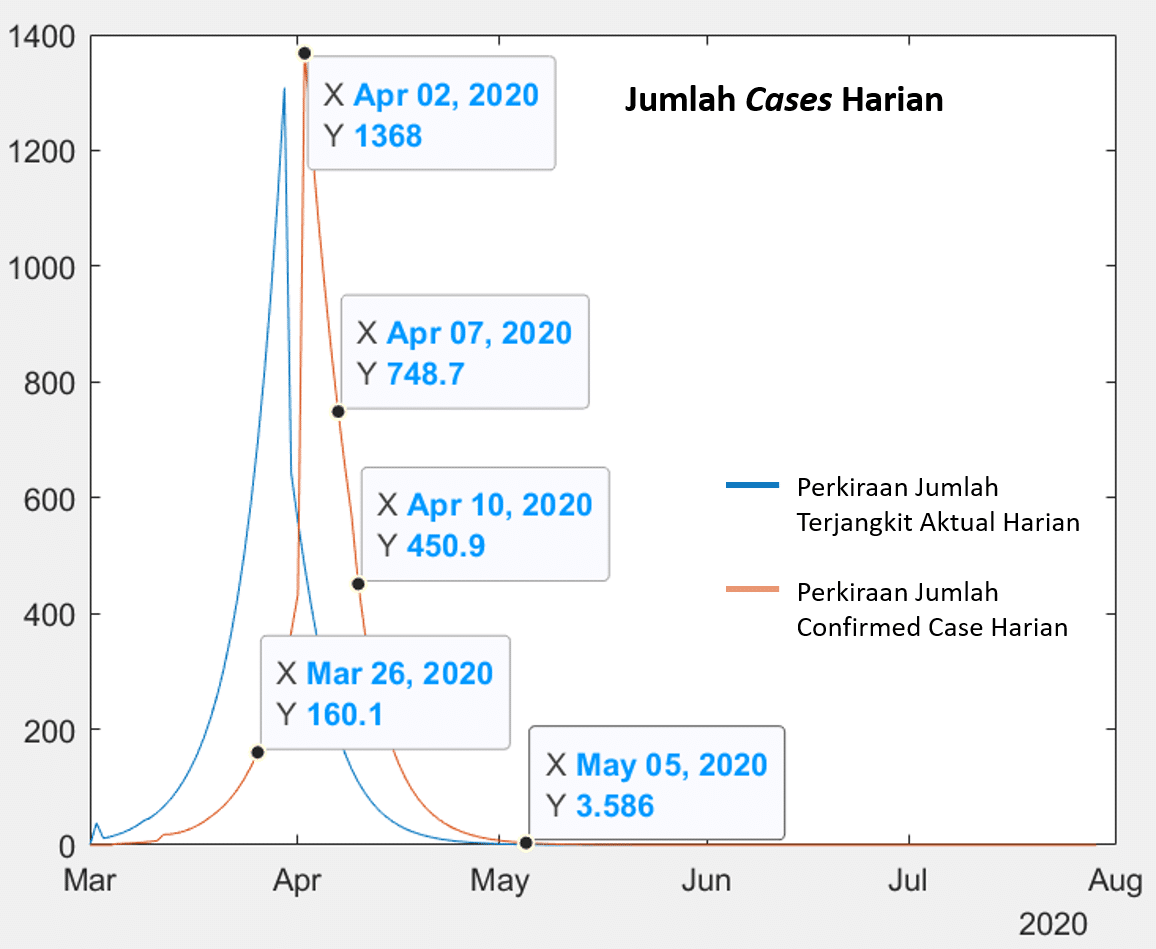
Dari simulasi dapat kita lihat bahwa dengan menjalankan skenario ini, siklus wabah akan berakhir pada minggu pertama Mei dengan batas atas akumulasi confirmed_case adalah di sekitar 12750 orang. Puncak siklus akan terjadi di tanggal 2 April dengan maksimum confirmed case harian adalah 1368.

5. Perkiraan Jumlah Terjangkit Aktual di Luar Confirmed Case

Di bab 1 dari tulisan ini sudah dijelaskan mengenai adanya asumsi delay dalam dirilisnya confirmed case. Delay diasumsikan sangat moderat hanya selama rata-rata tiga hari. Delay ini adalah jeda waktu sejak saat dilakukannya tes terhadap seseorang (suspect), yang kemudian dinyatakan positif, hingga konfirmasi resmi pemerintah yang  memasukkan orang tersebut ke dalam akumulasi total terjangkit. Semakin panjang delay actual maka semakin besar gap antara confirmed case yang diumumkan dengan kondisi aktual.

Selain itu, deteksi terjangkit positif yang berlanjut sampai isolasi diasumsikan hanya dapat menjaring 40% terjangkit setelah fase inkubasi. Ini karena dalam masa inkubasi (fase pertama yakni 7 hari pertama) peluang keberhasilan deteksi sangat rendah terhadap seseorang yang aktualnya telah terjangkit. Selain itu, berdasarkan pernyataan beberapa sumber,  terdapat 40% – 60% terjangkit aktual yang hanya menampakkan gejala sakit sangat ringan atau bahkan tanpa gejala sama sekali.

Apa akibatnya? Akan ada gap antara jumlah akumulasi confirmed case yang dilaporkan dengan banyaknya terjangkit aktual. Berikut ini adalah grafik hasil perkiraan jumlah aktual akumulasi terjangkit, disandingkan dengan hasil simulasi confirmed case beserta data empiris confirmed case. Berikut ini akan ditunjukkan terlebih dahulu keselarasan antara hasil simulasi confirmed_case dengan data empiris confirmed case.

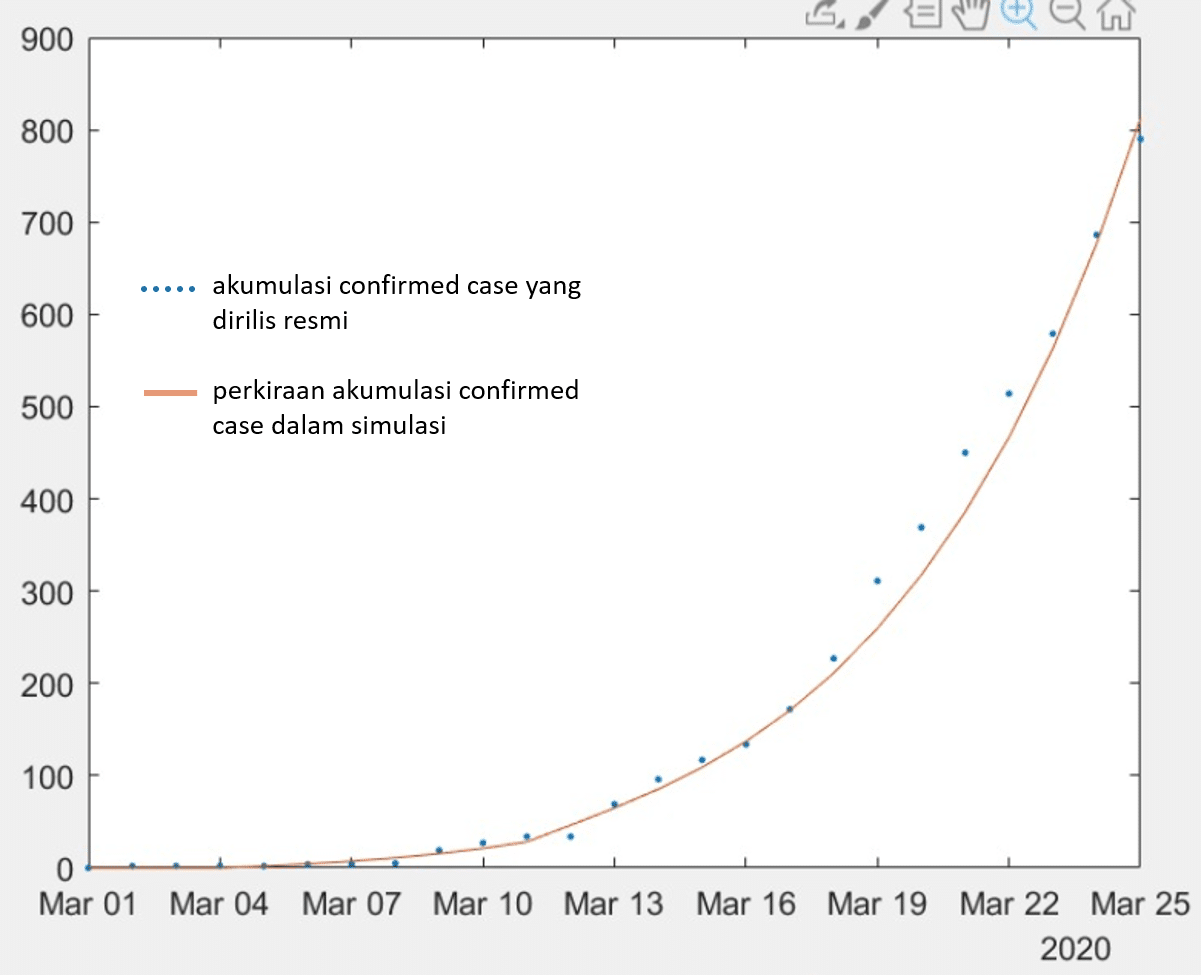
Gambar 6. Keluaran confirmed case model (merah) disandingkan dengan data empiris (biru)

Berdasarkan keselarasan tersebut, berikutnya akan kita lihat perkiraan jumlah terjangkit disandingkan dengan data confirmed case yang dirilis pemerintah.

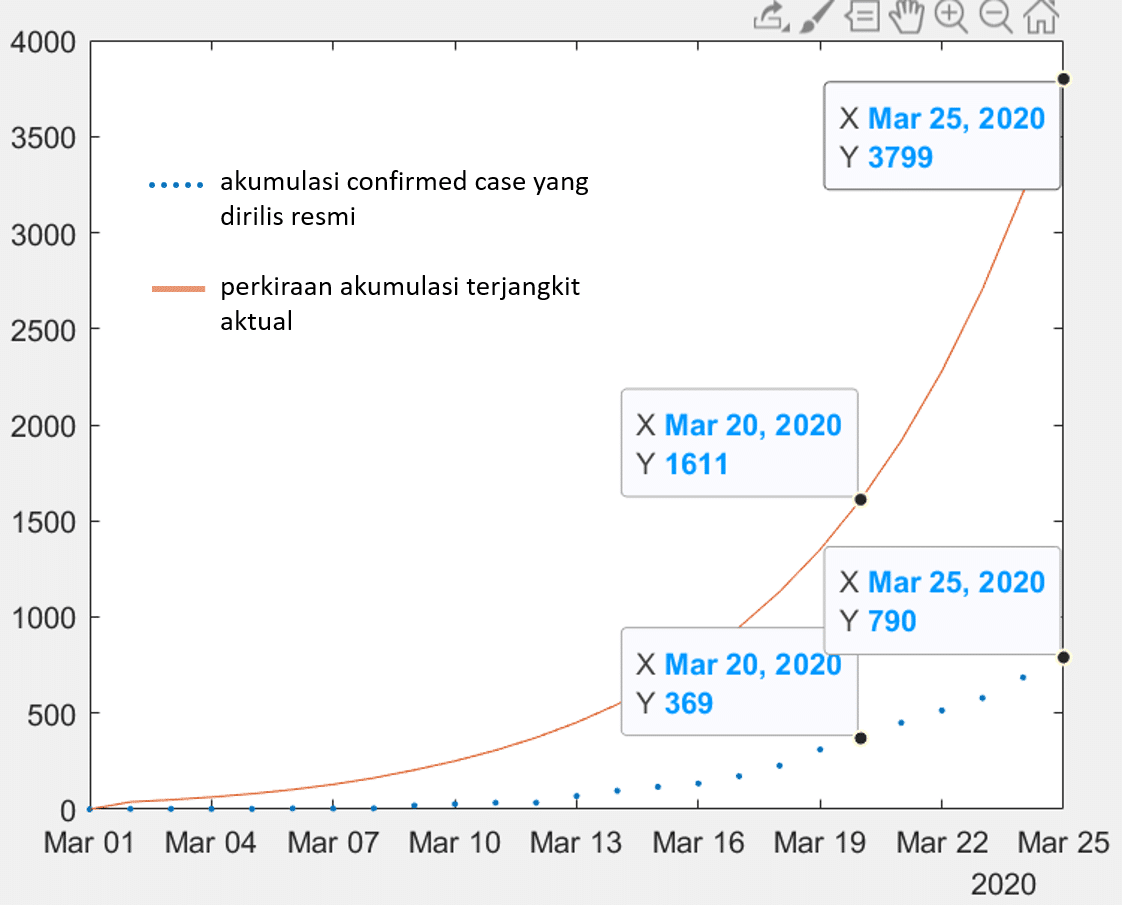
Gambar 7 Perkiraan jumlah terjangkit aktual (merah) disandingkan dengan confirmed case yang dirilis resmi.

Berdasarkan hasil simulasi yang ditampilkan di Gambar 7, kita dapat memperkirakan banyaknya terjangkit aktual yang jumlahnya dapat mencapai lima kali lipat angka confirmed case yang dilaporkan. Sekitar 40% – 50% terjangkit aktual ini diduga adalah terjangkit yang memang hanya menampakkan gejala sangat ringan atau bahkan tanpa gejala sehingga sulit dideteksi. Sebagian lainnya adalah terjangkit yang telah masuk daftar ODP, PDP. Di luar itu adalah terjangkit yang mengalami gejala ringan hingga menengah yang belum datang untuk berkonsultasi ke rumah sakit. Perkiraan angka terjangkit aktual ini dapat kita gunakan sebagai panduan untuk merencanakan pelaksanan rapid test.

6. Kesimpulan

Berdasarkan simulasi di atas, beberapa hal yang perlu segera ditindaklanjuti dalam merumuskan strategi penanganan ke depan adalah sebagai berikut:

1. Skenario physical distancing yang ketat diharapkan dapat secara efektif menekan jumlah confirmed casei dan sekaligus memperpendek siklus wabah. Kita perlu terus memantau efektifitas implementasi strategi ini. Terlalu longgar sedikit saja maka hasil akhir bisa sangat jauh berbeda. Simulasi di atas menunjukkan hasil yang sangat jauh berbeda antara physical distancing hingga 1/5 kali (ketat) dengan physical distancing hanya 1/2  kali (moderat). Dalam hal ini , pemerintah dan masyarakat perlu bahu membahu memaksimalkan physical distancing dan mencegah kegiatan-kegiatan yang bersifat anti physical distancing .
2. Skenario peningkatan cakupan deteksi dan isolasi hingga mencakup 20% orang terinfeksi yang masih berada di fase awal (minggu pertama), 50% terinfeksi di fase tengah dan akhir (minggu kedua, ketiga dan keempat). akan menghasilkan efek yang serupa dengan physical distancing. Skenario meskipun tampaknya dapat mempercepat puncak siklus namun masih menghasilkan durasi siklus yang panjang. Skenario ini perlu diperkuat dengan teknologi early warning system yang dapat mendeteksi orang-orang yang berisiko tinggi (pernah kontak dengan orang yang positif, ataupun rantai kontak berikutnya). Ini bisa dilakukan misalnya , selain dengan penerapan teknologi rapid mass test, juga  dengan menggunakan aplikasi teknologi informasi dan big data maupun machine learning.
3. SImulasi juga menunjukkan bahwa strategi gabungan, physical distancing dan peningkatan cakupan deteksi, memberikan hasil yang dapat menekan angka maksimum terjangkit dan memperpendek durasi siklus wabah. Strategi gabungan ini mencakup: physical distancing moderat + perluasan isolasi dan deteksi.
4. Seluruh langkah di atas mestinya juga dibarengi dengan langkah untuk mencegah terjadinya imported case baru. Karakteristik sistem dinamik penularan virus yang memiliki struktur umpan balik positif menghasilkan sistem yang tidak stabil di titik ekuilibrium nol. Artinya, masuknya imported case baru senantiasa berpotensi menghasilkan rantai penularan baru yang bisa sangat sulit dikendalikan.
5. Mengingat bahwa setiap kota atau propinsi bisa dimodelkan dengan model dinamik yang mirip, maka pencegahan imported case antar daerah, khususnya dari daerah yang menjadi episentrum saat ini seperti Jakarta dan Jawa Barat ke daerah-daerah lain, perlu dicegah dan diminimalisasi. Dalam hal ini, penulis merekomendasikan agar pemerintah meminimalkan arus mudik lebaran dan hari raya lain selama wabah ini belum berlalu.

Berikut adalah tabel yang meringkas hasil simulasi beberapa skenario:

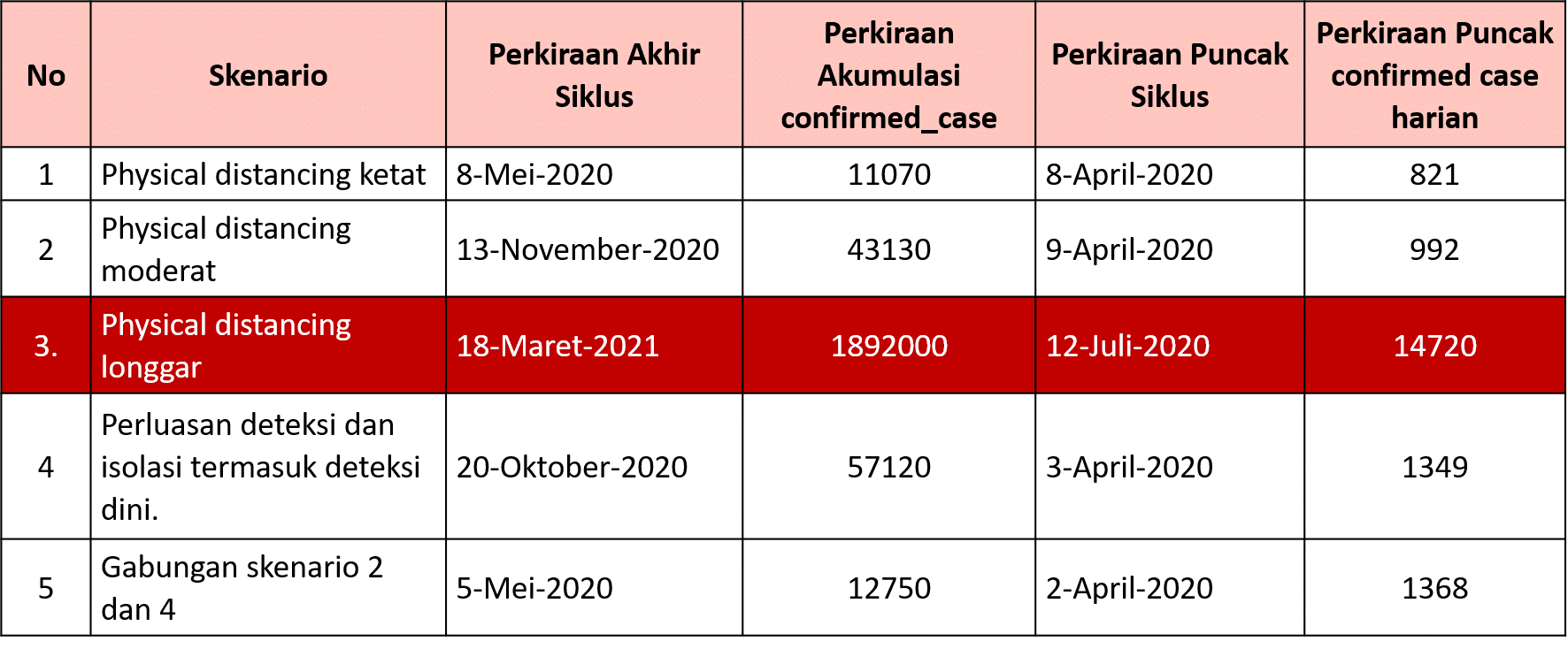
Selain itu terlihat bahwa angka perkiraan akumulasi terjangkit aktual bisa sampai lima kali lipat akumulasi confirmed case yang dilaporkan pemerintah. Ini bisa dilihat di tabel berikut ini:

7. Lampiran

Model dinamik dibangun berdasarkan pengetahuan mengenai perilaku penyebaran virus sebagai berikut:

1. Penambahan jumlah terjangkit virus corona secara alamiah akan mengikuti deret geometri atau dengan kata lain menampakkan perilaku eksponensial. Akumulasi jumlah terjangkit di suatu hari adalah kelipatan dari jumlah terjangkit di hari sebelumnya.
2. Seseorang yang terjangkit tidak selamanya menularkan virus. Orang tersebut hanya akan menjadi vector penularan hanya dalam rentang waktu tertentu, yaitu selama dia terinfeksi virus. Setelah melewati masa itu dengan selamat, orang tersebut tidak akan menularkan lagi virus ke orang lain.
3. Orang akan kebal setelah sembuh dari infeksi virus. Beberapa sumber mengatakan bahwa kekebalan ini hanya berlangsung temporal. Belum terlalu jelas berapa lama kekebalan ini bertahan. Namun sejauh ini, berulangnya kasus terjangkit pada orang yang sama dianggap sangat minim berdasarkan pada data penurunan jumlah terjangkit setelah dilakukan . Berdasarkan pengetahuan mengenai virus yang serupa, kekebalan ini tampaknya berlangsung cukup lama, sehingga dalam rentang waktu siklus yang sedang berlangsung saat ini kita masih dapat mengasumsikan bahwa orang yang terjangkit dan sembuh selanjutnya akan kebal.
4. Bertambahnya jumlah terjangkit dalam suatu populasi dapat disebabkan oleh dua hal, yaitu (i) tertular oleh orang yang telah terjangkit sebelumnya dari populsi yang sama, atau (ii) tertular oleh orang dari luar populasi. Kasus (i) dalam model akan menghasilkan pelipatgandaan. Kasus kedua dinyatakan sebagai imported_case atau tambahan kasus baru dari luar.

Kita menggunakan pengetahuan di atas sebagai asumsi untuk membangun model dinamik. Berikut adalah gambaran (simplified) model tersebut.

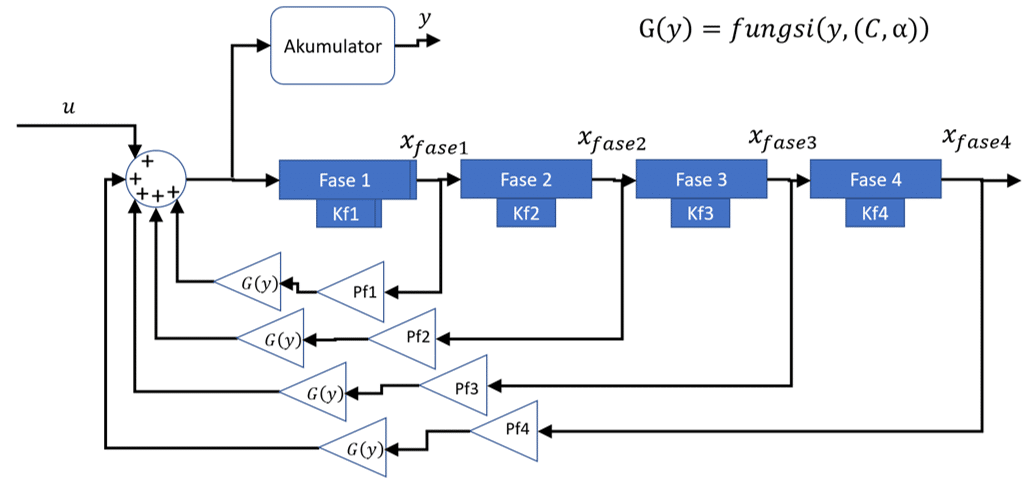
Gambar 8 Skema dasar model system dinamik penularan virus.

Penjelasan symbol-simbol dalam model:

• Variabel X_fase1 , …, X_fase4 menyatakan vector yang menyatakan jumlah terjangkit yang berpotensi menularkan virus di masing-masing fase di hari tertentu.
• Parameter K_{f1, …,} K_f4 menyatakan proporsi terjangkit pada fase tertentu yang secara aktual menularkan virus.
• Parameter P_{f1, …,} P_f4 adalah konstanta pengali yang menyatakan berapa rata-rata banyaknya orang yang dapat tertular oleh seorang terjangkit dalam satu hari untuk setiap fase.
• Vektor u menyatakan  banyaknya terjangkit baru yang berasal dari luar populasi. Vektor u ini juga dapat menyatakan terjangkit baru dalam populasi yang tertular oleh orang dari luar populasi. Vektor y, yang berdimensi satu, menyatakan akumulasi total orang yang telah terjangkit dalam populasi, baik yang masih dalam keadaan sakit, sudah sembuh ataupun meninggal. 
• G(y) adalah fungsi nonlinear variabel y yang digunakan sebagai faktor pengali dalam jalur umpan balik sistem. Fungsi G(y) merupakan faktor pengali dalam umpan balik yang menggambarkan pengaruh semakin banyaknya akumulasi orang terjangkit ke kecepatan penularan.
• C konstanta yang menyatakan batas atas banyaknya orang dalam populasi yang berisiko tertular.
• α adalah parameter dalam fungsi G(y) yang mendefinisikan kondisi akhir jumlah terjangkit dalam populasi jika kondisi penularan virus dibiarkan berlangsung begitu saja tanpa kontrol.

Skema di atas menggambarkan bahwa model dinamika sistem memiliki umpan balik positif. Apa artinya? Ini artinya jika ada satu saja orang terjangkit masuk ke dalam populasi, maka satu orang tersebut akan membangkitkan terjangkit baru dan selanjutnya akan terbentuklah pelipatgandaan akumulasi jumlah terjangkit. Kecepatan pelipatgandaan ini bergantung pada nilai konstanta P dan K dari sistem. Grafik berikut menunjukkan apa yang terjadi ketika suatu populasi mendapatkan satu orang terjangkit pada hari ke 20.

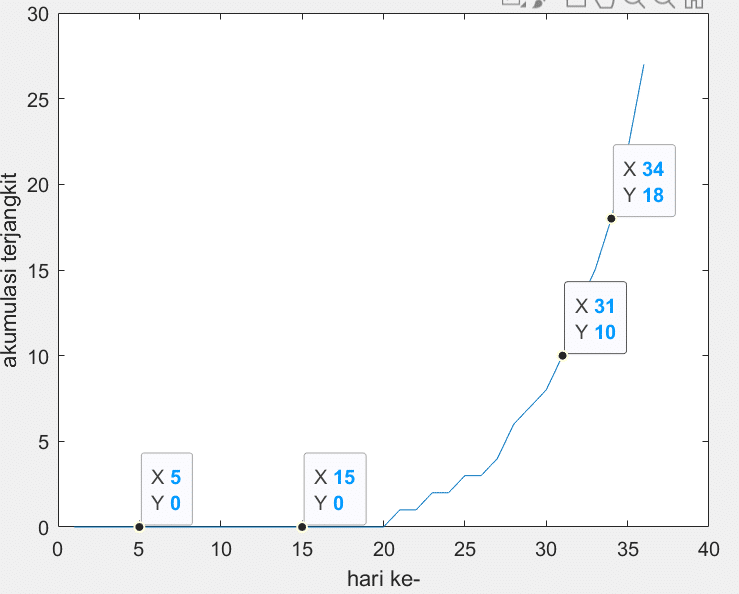
Gambar 9 Simulasi masuknya terjangkit baru di hari ke-20. Sumbu X menyatakan hari dan sumbu y menyatakan akumulasi terjangkit

Model juga rentang masa infeksi virus ke dalam empat fase. Parameter P dan K dapat diatur sedemikian rupa sehingga merepresentasikan kondisi paling realistis penularan virus dalam masing-masing fase. Sebagai contoh, dalam fase-1 kecepatan penularan oleh seorang yang telah terjangkit akan cenderung lebih tinggi. Mengapa demikian? Dalam fase ini, seseorang yang terjangkit belum mengalami gejala apapun sehingga dia akan melakukan aktifitas sehari-hari sebagaimana biasa yang banyak berinteraksi dengan orang lain. Berbeda dengan fase-1, dalam fase-2 sebagian orang yang terjangkit akan menunjukkan gejala sakit. Aktifitas mulai sedikit terganggu. Kecepatan penularan cenderung menurun di fase ini. Demikian pula, di fase-3 dan fase-4, kita dapat memberikan konstanta P yang kita anggap cukup realistis menggambarkan kondisi di fase ini. Model sementara mengasumsikan rentang waktu infeksi paling lama 30 hari. Setelah itu orang yang terjangkit tidak lagi berpotensi menularkan virus karena sudah sembuh ataupun meninggal. Untuk saat ini, penulis hanya menggunakan informasi yang masih sangat minim untuk memberi nilai setiap parameter tersebut. Ketepatan parameter juga nantinya dapat diverifikasi secara empiris dengan membandingkan keluaran sistem dengan dinamika empiris penyebaran virus baik di Indonesia, negara lain, ataupun angka total secara global.